ケインズの失業図
1
ケインズの『雇用・利子および貨幣の一般理論』(以下『一般理論』と略す)が出版されたのは1936年である。私が大学で経済学を学んだ頃はケインズ全盛であり、『一般理論』は必読書であった(私もゼミで原書を読んだ)。その後、フリードマンたちマネタリストの興隆や新古典派の復活によって、ケインズの理論は見捨てられてしまったようだ。経済学者ではない私は学界には疎いのだが、もはや『一般理論』そのものは経済学史の対象としてのみ扱われているのであろう。しかし、その解釈については謎が残されたままであると私は思う。
というのは、私にはずっと疑問に思っていたことがあったからだ。私たちが解説書などによって教えられてきたケインズ雇用理論は、図1を使って示されている(wは貨幣賃金、pは物価、Nは雇用量、Dは労働需要曲線、Sは労働供給曲線)。
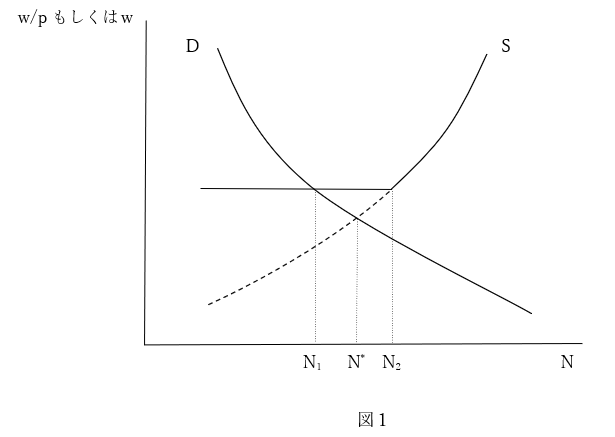
一般によく見られる需要・供給図と同様、労働需要曲線は右下がり、労働供給曲線は右上がりであるが、労働供給曲線の下端が水平になっている。つまり、この図では労働供給曲線がある賃金水準以下には下がらないことになっている。賃金の下方硬直と呼ばれる想定である。本来需要と供給が一致する点(完全雇用均衡点)で賃金と雇用量が決まるのであるが、賃金の下方硬直により、労働の超過供給(N2-N*)と過少需要(N*-N1)が生じている(N*は完全雇用量)。この労働の需給の差(N2-N1)、あるいは(正しくは)過少需要が非自発的失業であるとされている。
古典派は労働需給を実質賃金の関数とするから、もし失業があるのなら実質賃金が高いからであり、それが下がれば労働需要が増加し労働供給が減少して、その状態が解消されると主張する。したがって、賃金の下方硬直があるのであれば、そのことが失業を発生させていることになる。この図はいわばケインズの新古典派的解釈であり、ケインズの革新性は表わされてはいないのである。
ケインズが主張するように、彼の理論が古典派理論とは決定的な違いがあるのなら、この図による解釈は間違っているように思える。では、どのような図でケインズ雇用理論を表現すればいいのだろうか。『一般理論』を再読してみて一つのアイデアを得たので、ここに提示してみる(ただし、以下で検討するのは、ケインズが正しかったかどうかではなく、ケインズがどのように理解されるべきであったかについてである)。
2
ケインズは「非自発的失業」を次のように定義している。(引用文の頁数は塩野谷九十九訳『雇用・利子および貨幣の一般理論』〈東洋経済新報社、第四版、1950年〉による)。
もし、賃金財の価格が貨幣賃金に比してわずかに騰貴した場合に、その時の貨幣賃金で働こうと欲する総労働供給と、その賃金で雇おうとする総労働需要がともに、現存雇用量よりも大であるならば、人々は現に非自発的に失業しているのである。(18頁)
「賃金財の価格が貨幣賃金に比してわずかに(small)騰貴」するというのは、実質賃金が下落することである。素直に読めば、不完全雇用(非自発的失業の存在)下では、実質賃金の下落によって雇用量が増加するとケインズは言っている。実質賃金が下落すれば労働需要が増えるというのは理解できる。しかし、労働供給はなぜ増えるのであろうか。
この解釈として、労働者の貨幣錯覚ということが提唱された。労働者が考慮するのは貨幣賃金であり、多少の物価変動は気にしないので、物価の上昇による実質賃金の(ある程度の)下落は無視する。それゆえ、たとえ実質賃金が下落しても、貨幣賃金が変わらなければ、労働供給は減少しない。一方、実質賃金の下落は労働需要を増加させる。もし、その時点での貨幣賃金水準で働くことを希望する失業者が多数いたとしたら(賃金の下方硬直)、実質賃金の下落にもかかわらず雇用量が増加する。この雇用量の増加によって非自発的失業者が減少する。
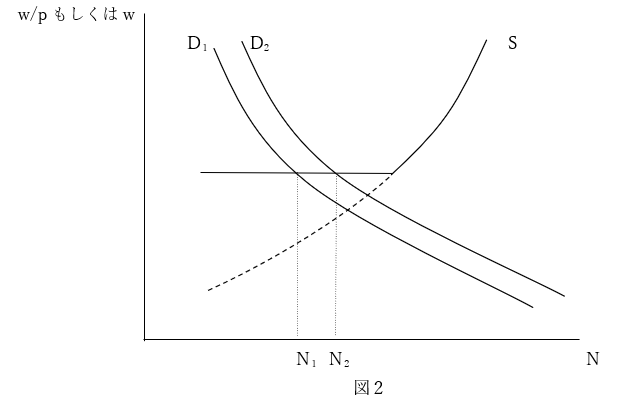
図2は貨幣錯覚と賃金の下方硬直による雇用量変化を表している。物価pの上昇(実質賃金の下落)により、Dは右方へシフトする(D1→D2)。一方、供給曲線Sは反応しないので、Sの水平部分に交点がある場合には、wは変化しない(つまり、実質賃金は低下する)のにもかかわらず、雇用量は増加する(N1→N2)。
しかし、貨幣錯覚を想定する限り、この図のようにはDとSを同時には描けない。これは簡単な理屈である。労働需要関数をN=f(w/p)、労働供給関数をN=g(w)とするならば、変数はN、p、wの三つであるのに、方程式は二つしかない。これでは解は決まらない。古典派のように労働供給関数をN=g(w/p)とするならば、w/pを一つの変数とすることができるので、変数は二つに減る。
考えられるのは、pをパラメータとすることである。pをパラメータとすれば図2が描け、pの変化はDのシフトとなる。
ところで、SとDの交点は完全雇用均衡点である。pの変化によるシフトは、ある完全雇用均衡点と他の完全雇用均衡点の違いでしかない。雇用が増えようと減ろうと、そこでの失業は全て自発的失業なのである。
確かにSの下方硬直部分が交点である場合では同じ賃金水準で雇用される者と失業する者が出てくる。しかし、期待できる賃金が低いために失業しているのは自発的失業である。それよりも低い賃金を受け入れることで雇用されるのが可能であるならば、そうしないことを労働者が選択していることになるからだ。それは下方硬直部分であろうとなかろうと同じことである。
図2においては、Sの下方シフトによっても雇用量が増加する。Sに下方硬直があろうとなかろうと同じことである。要するに、労働者が実質賃金の低下を受け入れれば雇用量は増えるということに過ぎないのだ。
貨幣錯覚と賃金の下方硬直という設定によって非自発的失業を解釈するために描かれたこの図は、説明に失敗している。そもそも古典派の体系では完全雇用均衡以外の均衡は考えられていないので、不完全雇用均衡というような概念を受け入れる余地はないのである。
ケインズの言うように、不完全雇用下で労働者が実質賃金の下落を受け入れるのは、その時点での実質賃金が労働の限界不効用よりも高いからである。ではなぜ古典派的には不均衡ともいえるそのような状態が出現するのか。雇用における競争が制限されていなければ、そのような状態は解消されて完全雇用(実質賃金=労働の限界不効用)が成立するのは当然のことのように思える。しかし、ケインズは雇用量は労働市場では決まらないと主張したのだ。他の市場の状況で労働需要が不足するならば、完全雇用を下回った水準で雇用量が均衡してしまうのである。
それゆえ、ケインズは「古典派の第二公準」を否定した。つまり、通常想定される労働供給関数を否定したのである。不完全雇用(実質賃金>労働の限界不効用)下では、労働需要が増加するならば、実質賃金が低下しても労働供給はなされる。労働供給が労働需要を常に満たすとすれば、労働需要曲線のみが存在することになる。では、労働供給曲線はどのように描かれるべきなのか。
3
ケインズは次のように言っている。
かくして、一定の実質賃金のもとにおいて使用可能な労働総供給量が雇用の極大水準を画するかぎりにおいては別であるが、それ以外には、雇用量は実質賃金をもって測られた労働の限界不効用によって決定されるものではない。消費性向と新投資率とが相俟って雇用量を決定するのであって、雇用量は実質賃金の一定水準に一義的に結び付けられる――その逆の関係ではないのである。もし消費性向と新投資率とが不十分な有効需要しかもたらさないならば、現実の雇用水準は現存実質賃金で潜在的に使用可能な労働供給に達しないであろう。そして均衡実質賃金は均衡雇用水準の限界不効用よりも大であるであろう。(35頁)
各雇用水準と、その水準における労働の限界不効用と等しい実質賃金の関係の軌跡が、通常の労働供給曲線である。言いかえれば、通常の労働供給曲線上の実質賃金はその雇用水準での労働の限界不効用に等しい。労働者は限界不効用が実質賃金と等しくなるまで労働を供給することによって利得を最大にすることができるからである(実質賃金が労働の限界不効用よりも高い状態では、労働者はさらなる利得を得る機会を失っている)。「現実の雇用水準は現存実質賃金で潜在的に使用可能な労働供給に達しない」というのは、均衡点が通常の労働供給曲線から外れているということであり、それゆえ「均衡実質賃金は均衡雇用水準の限界不効用よりも大である」のである。
だからといって通常の労働供給関数が全く不要ということにはならない。なぜならば、完全雇用の概念にはそれが必要だからである。「一定の実質賃金のもとにおいて使用可能な労働総供給量が雇用の極大水準を画する」のが労働供給関数なのである。その実質賃金水準ではさらなる雇用拡大はできない、あるいはその雇用水準での実質賃金以下ではその雇用水準を保てないというのが、その意味であろう。労働供給関数は雇用の可能な範囲を画している制約条件と考えるべきである。労働供給関数をg(w/p)=N、労働需要関数をf(w/p)=Nとすれば、g(w/p)≧f(w/p)=Nである。
通常の労働供給曲線上だけではなく、そこから離れた領域も均衡点として実現可能性があるのであれば、労働供給は面的に(範囲として)捕えなければならないことを意味している。労働供給関数とは、各実質賃金水準において許容しうる雇用量を表しているのであって、それを超える雇用は不可能であるが、それ以下の雇用は可能であることを示すものである。
したがって、ケインズの失業概念は図3のように描かれる。不完全雇用下の雇用量がN1である。この雇用量は完全雇用量(N*)を下回っているから非自発的失業(N*-N1)が生じている。労働市場では労働需要曲線Dが需給一致を現すことになるが、雇用量は労働市場では決定できない。雇用量は財市場や金融市場との関係で定まる。雇用が増加する場合は、実質賃金が労働需要曲線に沿って下落することになるが、増加する労働需要を供給が常に満たすことになる。点線S(通常の労働供給曲線)は完全雇用を表しており、これを越すと労働供給が制限される境界である。
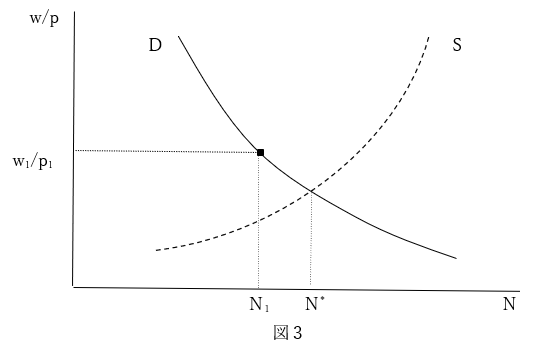
ケインズは雇用量は有効需要によって決まるとした。有効需要とは「企業者たちが、彼等の雇い入れようと決意する経常雇用量から、彼等が他の生産要因に対して支払うべき所得をも含めて、獲得すると期待する総所得(または売上金額)」(64頁)、あるいは、「期待された消費と期待された投資との総和」(293頁)である。
ケインズによれば、不完全雇用の状態においては、有効需要の増加は生産と雇用を増やす一方、限界生産力の低下により価格を上昇させ、実質賃金を低下させる。それにもかかわらず雇用供給は需要に応じて完全雇用に至るまで増加する。
4
賃金の下方硬直が自発的失業の主因とみなされてしまったことは、ケインズの説明の仕方にも責任があろう。ケインズは労働者が実質賃金よりも貨幣賃金の方にこだわるとか、貨幣賃金の非伸縮性ということを言っている。また、労働者は貨幣賃金の切り下げには抵抗するが、物価の上昇による実質賃金の下落には寛容であるので、後者の方が望ましいとも言っている。非自発的失業の概念の理解に苦しむ読者が、この記述に間違ったヒントを得てしまったのである。
ケインズの記述は言葉による説明に徹している。『一般理論』には図解が一つしかないのは有名である。図解ではものごとを単純化してしまい、現実の複雑さを見逃してしまうとケインズは考えていたのかもしれない。しかし、言葉による説明は逐次的であり、積み重なっていく内容をどのように関連づけるかが難しい。ケインズ自身は全体的な構図を持っているのだが、読者にそれが分かるのは読了してからである。ただし、私を含めた多くの読者は、読書中は迷路にいるようで、結局後から振り返ってもよく理解できていないままであるのではないか。図3によるケインズ雇用論の解釈はいささかなりとも助力になるであろう。
ところで、私の理解した限りでのケインズと古典派の違いは、大雑把に言えば以下の通りである。いわゆる「古典派の第一公準」をケインズも認めていたので、雇用の拡大には実質賃金の下落が必要ということになる。実質賃金(w/p)の下落には、物価(p)の上昇と貨幣賃金(w)の下落の二通りの過程がある。それらの変化は、均衡状態では内的な要因からは生じないので、何らかの外的な影響が想定されよう。
古典派では、物価の上昇あるいは貨幣賃金の下落のいずれにせよ、実質賃金の低下は生産の拡大(労働需要の増加)を促がすが、同時に労働供給を減少させる。労働供給を増やすためには実質賃金が上昇しなければならない。結局、それらの動きは相殺されて均衡からのかい離は押し戻されることになる。ただし、物価の上昇の場合は、均衡へ戻る際に貨幣賃金が上昇するならば、実質賃金が元通りになっても、物価と貨幣賃金は比例して上昇したままとなる(名目値の上昇、インフレ)。
ケインズも、完全雇用においては生産は拡大せず、有効需要の増加は価格と貨幣賃金の上昇をもたらすだけということを認めている。しかし、不完全雇用においては有効需要の増加が生産と雇用を増加させることができる(その過程で実質賃金が低下する)と主張する。
では、不完全雇用において、貨幣賃金が下落する効果についてははどうであろうか。貨幣賃金の下落による実質賃金の下落が直接に雇用量の増加をもたらすことはありうる。しかし、生産の増加に見合うように消費や投資が増加しなければ、物価が下落することによって需給バランスがとられなければならない。生産と雇用は元の水準に戻るだけでなく、デフレスパイラルに陥るかもしれない。
貨幣賃金の下落が雇用を増加させるとしたら、有効需要を通じてであるが、ケインズはそのことに否定的であった。したがって、労働者が貨幣賃金を下げることによって雇用を増大させることはできない。別の文脈で(インフレとデフレの非対称性)ではあるが、ケインズは以下のように述べている。
すなわち、労働者は常に当該雇用量の限界不効用以下での実質賃金を伴う規模において働くことを拒否する地位にはあるけれども、当該雇用量の限界不効用より大でない実質賃金を伴う規模において仕事の提供されることを要求する地位にはないという事実がそれである。(330頁)
後半の「当該雇用量の限界不効用より大でない(not greater than)実質賃金を伴う規模」とは労働供給曲線上(限界不効用=実質賃金)の雇用量を意味している。むろん厳密にはそれを超えた雇用量(前半の「当該雇用量の限界不効用以下(less than)での実質賃金を伴う規模」、ただし「以下」ではなく「未満」が正しい)を含むが、労働者は拒否するはずである。つまり、労働者は労働供給曲線を超えた雇用量は拒否できるが、労働供給曲線上にないときはそれに到達するすべはないのである。労働供給曲線は雇用量の限界を示すけれども、雇用量自体を示すものではない。
5
ケインズは雇用量がどのようなメカニズムで決定されると考えたのであろうか。分かりやすいように新古典派的な実物的理解をしてみよう。
wを貨幣賃金、pを物価、Nを雇用量とする。労働供給関数g(w/p)=Nは「古典派の第二公準」であるが、ケインズはこれを否定し、g(w/p)≧f(w/p)=Nという制約条件に代える。f(w/p)=Nは労働需要関数である。
ケインズは「古典派の第一公準」、つまり限界生産力説(利潤極大条件)は認めていたから、生産関数をF(N)とすれば利潤極大条件は次のようになり、これが労働需要関数であり、また生産物の供給関数である。
F´(N)=w/p ……… ①
一方、生産物の需要は消費cF(N)と投資Iからなる。cは消費性向である。
F(N)=cF(N)+I ……… ②
生産物のうち消費に回されなかった分{F(N)-cF(N)}を貯蓄SとみなせばI=Sである。②式を変形するとF(N)={1/(1-c)}Iとなる。{1/(1-c)}は投資乗数である。
投資は利子率rと資本の限界効率eによって決まる。
I=J(r,e) ……… ③
c、r、eをパラメータとすれば、変数はN、w/p、Iである。ただし、均衡の雇用水準は必ずしも完全雇用とはならないであろう。
『一般理論』のこのような解釈によって、ケインズの失業図の謎は解けただろうか。私はそう思うが、皆さんはどう判断するだろう。