スティーブン・ジェイ・グールド『がんばれカミナリ竜』の17章「光れ、大きなヒカリムシ」には、ニュージーランドのワイトモア洞窟で見られるヒカリムシの「地下プラネタリウム」と、夜空の星との、配置の違いについて述べられている。星はランダムであるが、ヒカリムシはなわばりのゆえに均等に位置する。星が何かの形を形成しているように見えるのはランダムな配置ゆえであり、ヒカリムシの均等な配置はそのような見え方をしないのである。その違いをコンピュータで再現した図が載せられている。四角に並べた小区画を、ランダムに塗りつぶした「星」と、ランダムではあるがまわりの区画が埋まっていない小区画を塗りつぶした「虫」の比較である。それ自体も興味深いのだが、私は「虫」の配置についての記述が気になった。

　そこには、「虫」の場合は「四つに一つの小区画を埋めることができる」とあった。それが理解できなかった。まわりが空白なら「九つに一つ」ではないのか。

　図を描いてみると、図１か図２のようになる。9区画の中心にいる虫は、周りの８つの空白の区画を他の虫と共有している。

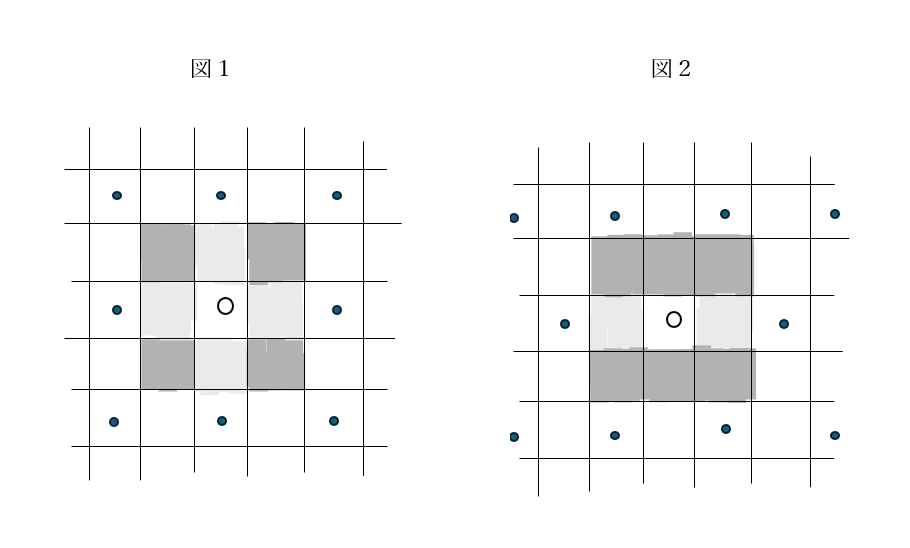
　図１の場合、８匹の虫を相手にし、４区画（濃い灰色）を他の３匹の虫と、４区画（灰色）を他の１匹の虫と共有し、１区画（白）だけは占有している。そこで、一つの区画の面積をａとして、この虫の取り分を計算してみると、

　（１／４）ａ×４＋（１／２）ａ×４＋ａ×１＝４ａ

　となって、この虫が支配しているのは正味4区画であることが分かる。

　図２の場合は、６匹の虫を相手にし、６区画（濃い灰色）を他の２匹の虫と、２区画（灰色）を他の１匹の虫と共有し、１区画（白）だけは占有している。したがって、

　（１／３）ａ×６＋（１／２）ａ×２＋ａ×１＝４ａ

　であり、やはり支配しているのは正味４区画となる。

　では、区画を三角形にしてみてはどうか。図３のように４区画に１匹の虫が配置されることになる。そのうち３区画（灰色）は他の二匹の虫と共有し、１区画（白）は占有である。この場合を計算してみると、

　（ａ／３）×３＋ａ×１＝２ａ

　となり、各虫が正味２区画ずつ支配していることになる。

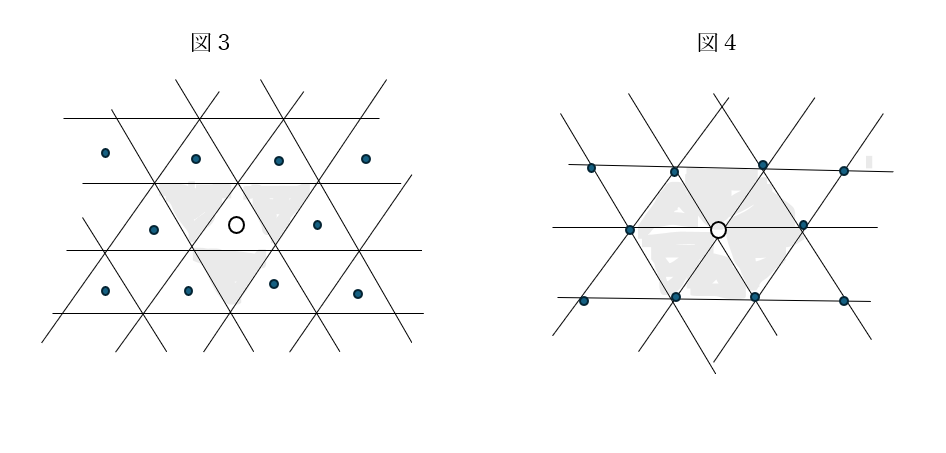
　四角形と三角形で所有する区画の数が違うのは、虫の密度が異なるからである。密度を考えやすくするために、それぞれの虫が境界線の交点にいると考えてみよう。図３の虫たちがそろって、たとえば占有する三角形の左下隅に移動したら、図４のようになる（つまり、図３と図４では虫の密度は同じである）。図４では占有する区画はなく、周りを取り囲む６匹の虫と６区画を共有することになり、正味支配区画の計算は（ａ／３）×６＝２ａとなる。

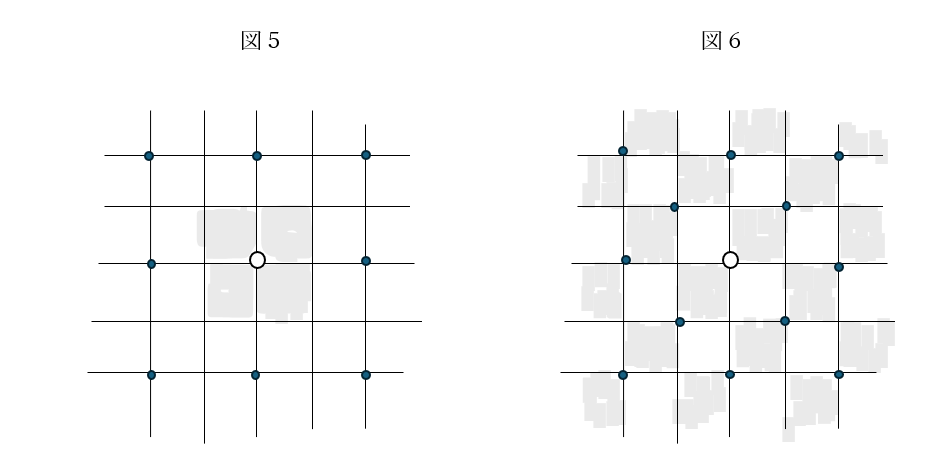
　四角形の場合も同様に、図１の虫たちが区画のどちらかの方向の境界線の交点に、たとえば四角形の左下隅に、そろって移動したならば、図５のようになる。この場合、虫たちはそれぞれ周りの４区画（灰色）を占有している（共有部分は生じない）。

　密度をあげるためにチェスボード型の配置を考えてみよう。市松模様の灰色の区画にそれぞれ虫がいるとして、それらが、たとえば占有する四角形の左下隅に、いっせいに移動したと考えるなら、図６のようになる。この場合、各虫の支配分は

　（ａ／２）×４＝２ａ

　となり、やはり正味２区画である。

　虫にとって適切な配置はどのようであろうか。妥当なのはお互いの距離を一定にすることであろう。したがって、図４のような配置となると考えるのがよいのかもしれない。

　ところで、虫が所有するのが区画ではなく面積であることにしてみよう。図４のような配置の場合に、一匹の虫はそれの周囲の六角形が内接する円を勢力範囲にしていると考えてみよう。この虫は、それを取り巻く６匹と、さらにその外側の６匹の計１２匹と勢力範囲を共有することになる（図７）。

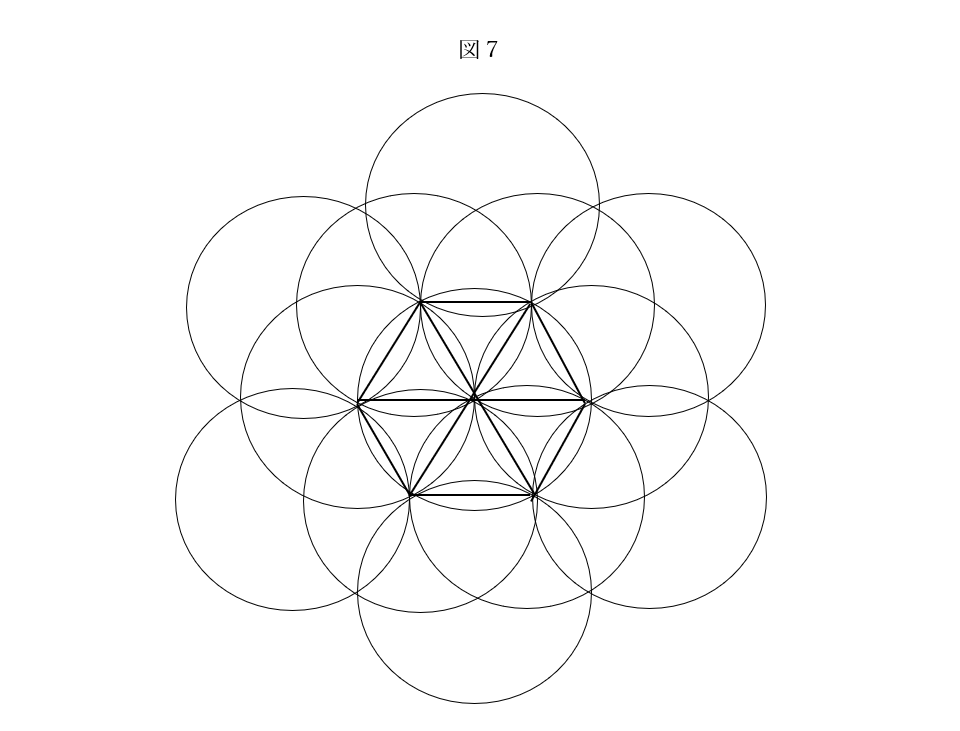
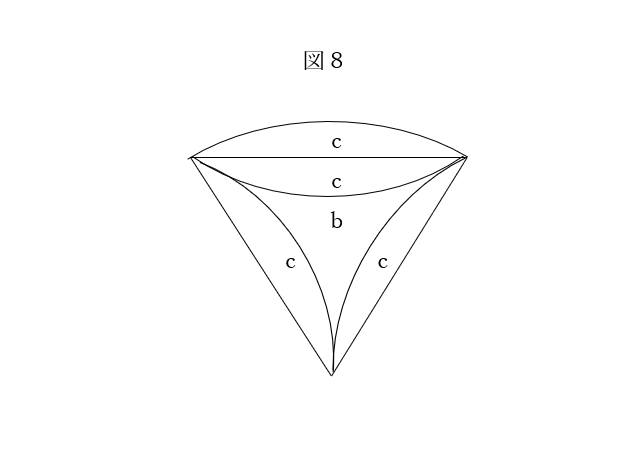
　六角形に外接する円の6分の1を図８に示した。面積ｂは3匹で共有され、面積ｃはいずれも4匹で共有されることになるから、各虫の支配する正味の面積は、

　（ｂ／３）×１＋（ｃ／４）×４＝（ｂ／３）＋ｃ

　となる。この部分が６つあるのだから、この虫の支配分は、

　（ｂ／３）×６＋ｃ×６＝２ｂ＋６ｃ＝２（ｂ＋３ｃ）

　となる。（ｂ＋３ｃ）は三角形の区画の面積だから、この虫はやはり２区画を支配していることになる。

　以上から、虫は一匹につき２区画を支配するというのが適切な表現ではないだろうか。