私は別の文章で、ケインズの『雇用・利子および貨幣の一般理論』（以下『一般理論』と略す）における労働市場の新古典派的解釈について批判的に検討した。新古典派的ケインズ解釈では、高賃金均衡という状況の説明に賃金の下方硬直という想定を使っている。それは誤ったケインズ解釈であるというのが私の主張であった。

　ところで、ここしばらくの日本の労働市場は、低賃金均衡とでも言うべき状態にあるようだ。賃金は上がらないのに、「人出不足」が続いているのである。いや、賃金が上がらないからこそ、「人手不足」が続いていると言うべきであろう。現行の賃金水準では、労働需要が労働供給を上回っているのに、賃金の上昇によってその「不均衡」が解消されることはないのである。本来であるならば、賃金の上昇により、労働供給は増え、そして、労働需要は減る。後者は、以前の賃金水準ではなされていた生産活動のうち、限界的な部分は市場から撤退することを意味する。市場が超過需要を解消しないのは、市場機能が損なわれているから、ということになるはずだ。この「不均衡の均衡」とでもいうべき状態を新古典派的に解釈してみたらどうだろうか。ケインズ解釈において賃金の下方硬直という仮定を採用したように、賃金の上方硬直という仮定を採用することになるだろう。

　労働供給曲線が上方で折れ曲がるということは考えられない。賃金が上がらないのに労働力が増加するということはないだろう。そういうことがあるのであれば、超過需要が解消されるか、供給が労働人口の限界に達することになるだろう。確かに少子高齢化による労働力不足は指摘されているが、そのことだけで「人手不足」を説明するのは難しい。

　だとすれば労働需要曲線の形状を検討してみるべきである。すなわち、労働需要曲線が上方で折れ曲がっているとするのである。これは奇妙なことかもしれないが、労働供給曲線が下方で折れ曲がっていることよりも奇妙すぎることはないだろう。そこで描かれるのが図１である（ｗは貨幣賃金、ｐは物価、Ｎは雇用量、Ｄは労働需要曲線、Ｓは労働供給曲線）。

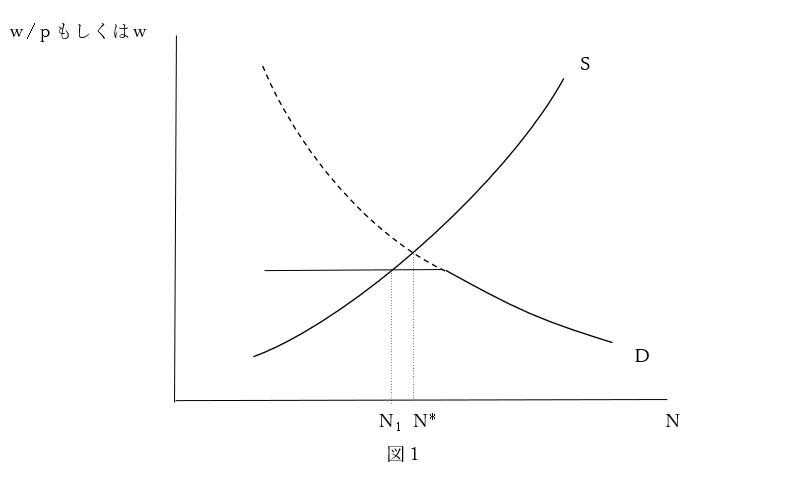
　さて、賃金の下方硬直という仮定を批判して、代替的に私が提案したのが、労働供給曲線を制約条件とみなすという方法であった。同じことを賃金の上方硬直に適用すれば、労働需要曲線の制約下に労働供給曲線上の点が均衡点になる（図２）。

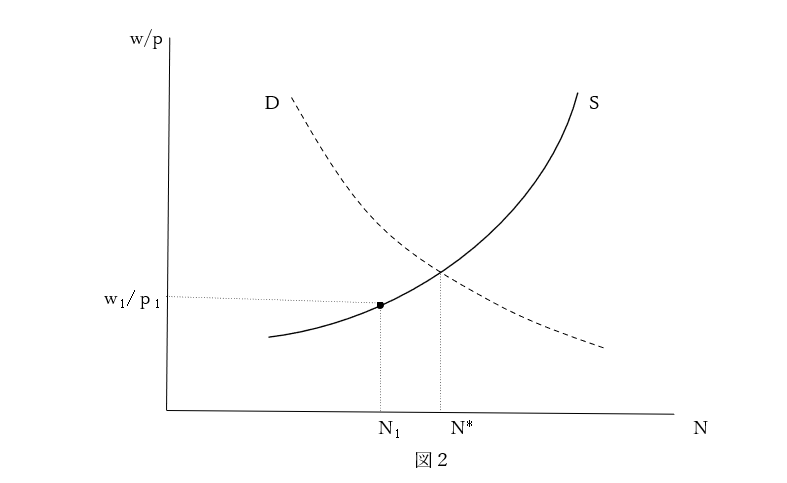
　しかし、賃金が完全雇用均衡値より高い場合には労働供給関数が制約条件になり、低い場合には労働需要関数が制約条件になるというのは、勝手すぎる解釈に思われる。

　ケインズの言いたかったことは、雇用量は労働市場では決定されないということであった。だとすれば、労働需要関数と労働供給関数の両方とも制約条件とみなすべきではないか。高賃金均衡と低賃金均衡が一般的に成立するのは、二つの制約条件が併存した場合に限られよう。とすれば、均衡点は、労働供給関数曲線上もしくは労働需要関数曲線上に位置するだけでなく、両曲線から離れたところにも位置することになる。それを図示すれば図３のようになるであろう。労働需要曲線と労働供給曲線にはさまれた斜線の部分（境界を含む）が均衡点の可能域である。

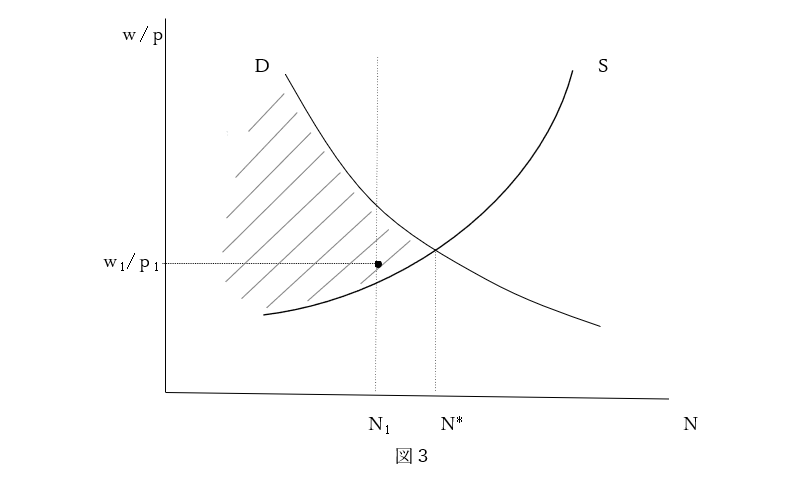
　ケインズは実質賃金の低下により雇用が増すのであれば、そのことは非自発的失業が存在していることを意味しているとみなした。それは、労働需要曲線上を完全雇用均衡点に向かって下がっていく動きである。しかし、図３の均衡点では、雇用が増加する経路において、実質賃金は上がるかもしれないし、下がるかもしれないし、そのままであるかもしれない。完全雇用均衡点が吸引力を持っているのではないからだ。

　ケインズは高賃金均衡を説明しようとしたので、低賃金均衡については視野に入っていなかった。高賃金であろうが低賃金であろうが、労働市場の需給は完全雇用均衡点以外で均衡することができると考えるのが、ケインズの正しい解釈であると思われる。

　この場合のケインズ体系は以下のようになるだろう。

　L(w/p)≧N、F´(N)≦w/pという制約条件のもとに、

　c、r、eはパラメータ、変数はN、w/p、 Iであるとすれば、この体系が決定されるには方程式が一つ足りない。そこで、w/ｐをパラメータとして扱う。労働市場においては、財市場と金融市場によって決定されたNと、パラメータであるｗ/pによって、均衡点が決まる。