ケインズの失業図について、第二公準を否定したケースと、さらに第一公準も否定したケースをそれぞれ検討してきた。今度は異なった角度から労働市場の均衡を考えてみよう。経済学的な解釈は保留して、単純にS・D曲線の片方を曲げてできる図を考えてみる。

　まず、①供給曲線が下方で、もしくは②需要曲線が上方で、水平に曲がるケースが挙げられる。形式的には逆のケース、③供給曲線が上方で、もしくは④需要曲線が下方で、水平に曲がっているケースも考えられる（図１）。

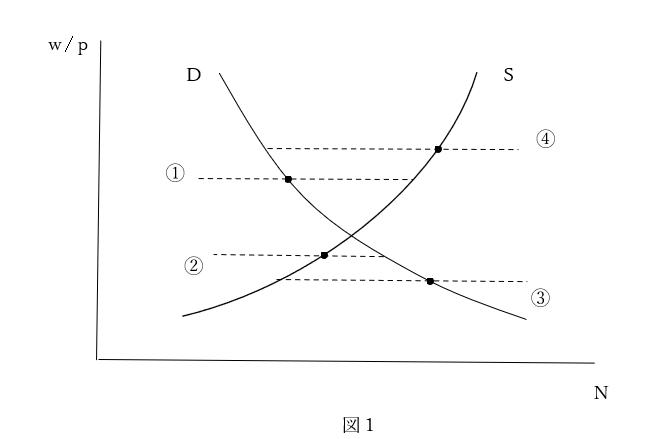
　では、垂直に曲がることは考えられるだろうか。形式的には水平に曲げた場合と同じように４つのケースが想定される。すなわち、⑤供給曲線が下方で、⑥需要曲線が上方で、⑦供給曲線が上方で、⑧需要曲線が下方で、垂直に曲がる（図２）。

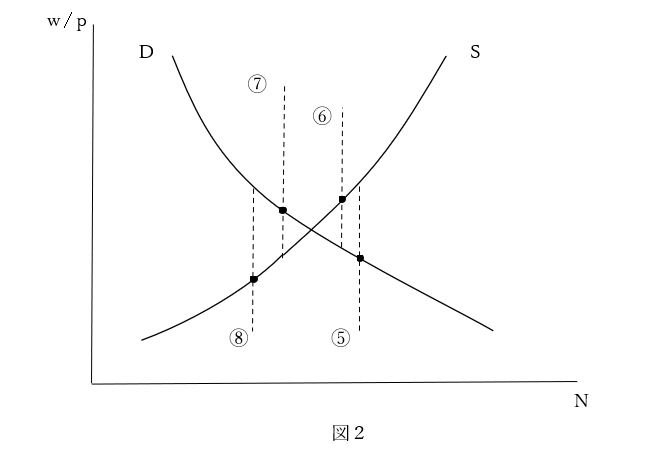
　⑦は非近代的（非合理的）な労働供給においてみられる現象として認められている。つまり、ある一定の額の賃金が得られればそこで労働をやめ、さらに賃金が上昇してもそれ以上の労働をしようとはしない態度である。労働の上方硬直とでも表現されようか。

　さて、この八つの均衡点を完全雇用均衡点との位置関係から、A（高賃金低生産）①⑦、B（低賃金低生産）②⑧、C（高賃金高生産）④⑥、D（低賃金高生産）③⑤の四つに分類し、労働需給曲線の上に位置づけてみよう（図３）。

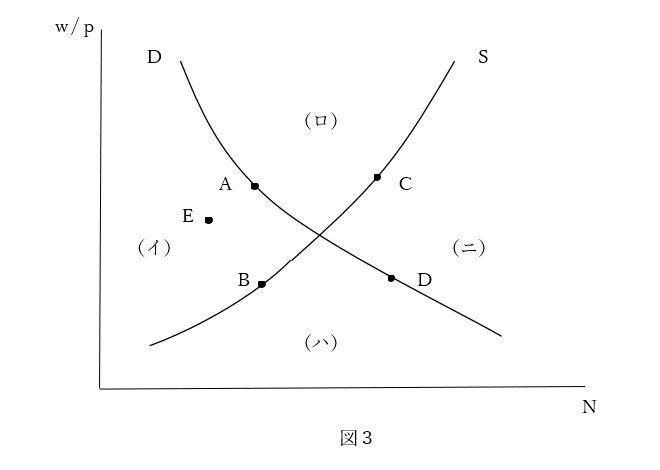
　このうち、CとDは何らかの強制力が伴わない限り実現不可能である。Cにおいては生産が、Dにおいて労働が利益の減少を被る。

　ではAとBはどうだろうか。Aにおいては、生産は需要曲線上にあって最適であり、労働は限界不効用以上の賃金を得ている。後者はさらなる労働の提供ができる機会を失ってはいるが、損失を被っているのではない。Bにおいては、労働は供給曲線上にあって最適であり、生産は限界生産力より低い賃金を支払っている。確かに、さらなる生産増によって得られる利潤の機会を逃してはいるが、損失を被っているのではない。つまり、AとBは自由競争において成立し得る均衡である。

　しかし、完全雇用均衡点よりも高い賃金では需要曲線上に均衡点があり、低い賃金では供給曲線上に均衡点があるというのは恣意的すぎるのではないか。それではＡとＢの存在を統一的に解釈することにならない。

　そこで、交差する需給曲線によって区分されるイ・ロ・ハ・ニの四つの領域を考えてみよう。（イ）は生産および／もしくは労働はさらなる利益の機会を失ってはいるが、両者とも損失は被っていない領域（境界も含む）である。生産も労働も自発的に行われ、自由競争がなされる領域と言っていい。（ロ）と（ハ）は生産と労働のどちらか一方が利益を減らしているか、場合によっては損失を被っている領域（左側の境界は含まず、右側の境界を含む）である。これは一方による他方の搾取の領域と言えるであろう。（ニ）は生産と労働の両者が利益を減らしているか、場合によっては損失を被っている領域（境界は含まず）であり、錯誤のようなことがない限りなされることはない。

　ケインズは新古典派の第一公準を認めていたため、彼が考えていたのはAのような均衡であった。しかし、第一公準をも否定すれば（イ）の領域のどこでも、例えばEのような位置にあることも可能なはずだ。

　『一般理論』の新古典派的解釈として、賃金の下方硬直を持ち出してきた人々は、供給曲線を曲げるという荒業を思いついた。そんなことを受け入れるのであれば、その荒業を徹底的に試してみるべきだった。そうすれば、賃金の上方硬直というアイデアに気がついたかもしれない。そして、賃金の下方硬直と上方硬直が同じ理論で説明されるべきならば、労働市場における供給関数と需要関数を値決定の関数としては扱えないことに思いいたったかもしれない。ケインズのように、あるいはケインズを越えて。